橫看成嶺側成峰－摩天大樓數獨之探討

羅依、蘇怡恩

摘要

摩天大樓數獨的每道題目由n×n表格及表格外的提示數組成，表格內的數字代表大樓高度，且數字排列須符合拉丁方陣之規則，而表格外的提示數代表從該方向可看到的大樓數量，較高的大樓會擋住後面較矮的大樓。本研究分別討論一維與二維表格，以及討論特定狀況的條件與計算符合的排列數量。

研究目的

1. 一維表格中，給定提示數及格數計算符合的排列數量
2. 一維及二維表格中，有唯一排列方式或無排列方式符合之充分或必要條件
3. 二維表格中，給定兩對側提示數後是否存在拉丁方陣

研究過程與方法

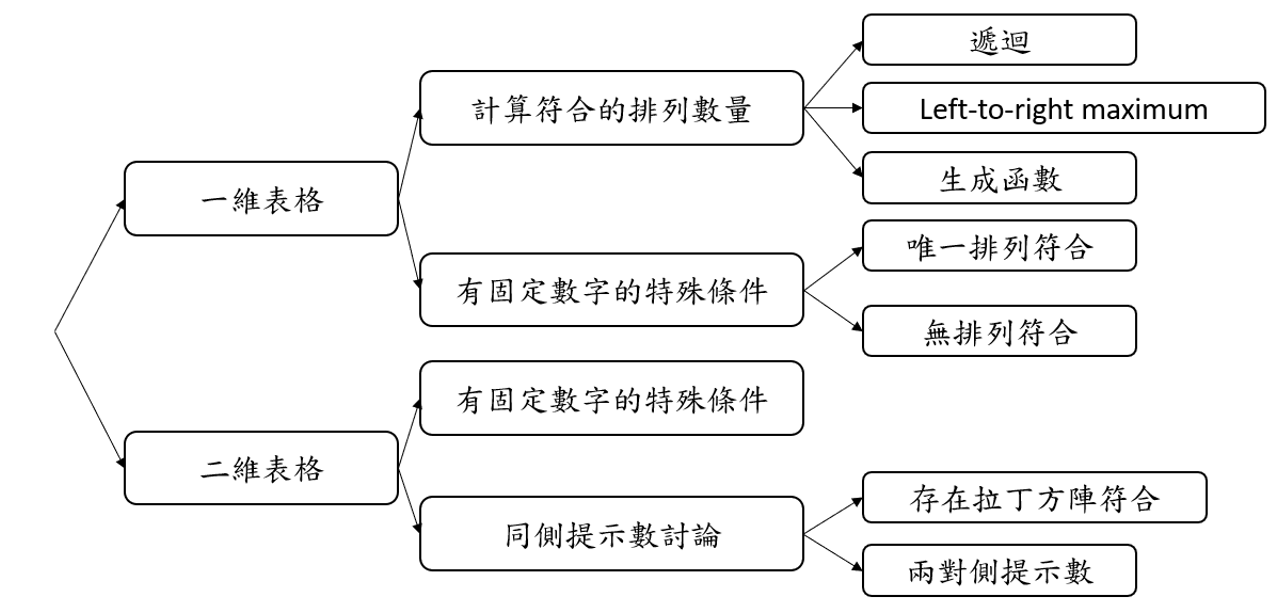
研究成果及展望

研究一維表格時，我們想計算符合的排列數量，於是我們分別往遞迴、生成函數的方向研究，並以程式輔助觀察，但在找出遞迴的解法後，我們對找出生成函數毫無頭緒，在閱讀資料時認識到新的知識 – Left-to-right maximum，並利用已知的知識研究出另一種遞迴方式，後來我們也利用程式跑出來的資料進行因式分解，找出生成函數。在研究有固定數字唯一或無排列符合的條件時，在寫程式列舉後，仍幾乎沒有觀察到整體性的規律，於是我們就分點研究每個特殊情況，整理出一些充分條件並列點呈現。

研究二維表格時，我們利用程式觀察後還是找不出四周提示數的關聯，於是我們先研究一側的提示數，並以依大小順序排列為分類方式，發現同側提示數存在的必要條件，也猜測同側提示數存在的數量和卡特蘭數有關。我們也觀察對側提示數，發現有兩同側提示數不能放在對側的情況，但並未發現規律，故以繪圖呈現。目前的研究結果較難直接判斷提示數填完後，是否有唯一的拉丁方陣可填入，未來希望可以找到有拉丁方陣可填入的決定性充分及必要條件。