Magic Poker ──撲克牌魔術揭密

邱鈺婷

摘要

在本篇研究中，我討論了不同張數、堆數下，藉由不斷選出目標牌，然後將它依規定疊合後重新發牌，試著找出其中規律。我發現在奇數堆的狀況下，奇數張牌時目標牌會藉由洗牌收攏至最終位置，而偶數張牌時則會循環，而偶數堆(n)的狀況下，每堆牌數為(n+1)的倍數張時，目標牌會循環，而各堆牌數非(n+1)的倍數張時，藉由洗牌能收攏至一最終位置。

未來想研究目標牌在不同情況下，移動至最終位置的最少步數與n.k之間的關係。

研究目的

1. 討論奇數堆各奇數張撲克牌時，目標牌洗牌後最終位置以及移動規律
2. 討論奇數堆各偶數張撲克牌時，目標牌洗牌後的循環規律
3. 討論偶數堆不同張數張撲克牌時，目標牌洗牌後最終位置、移動規律和循環規律
4. 討論不同堆數不同張數的牌洗牌後，移動至最終位置的最少步數

研究過程與方法

先以n的奇偶性分別討論n堆各k張牌時，目標牌的移動公式，接著以k分類討論其為循環或固定在目標位置，再進行證明其會逐漸靠攏至目標位置，並不會因為洗牌移動位置。

研究成果及展望

1. 奇數堆各奇數(2b+1)張撲克牌時，若目標牌為x，當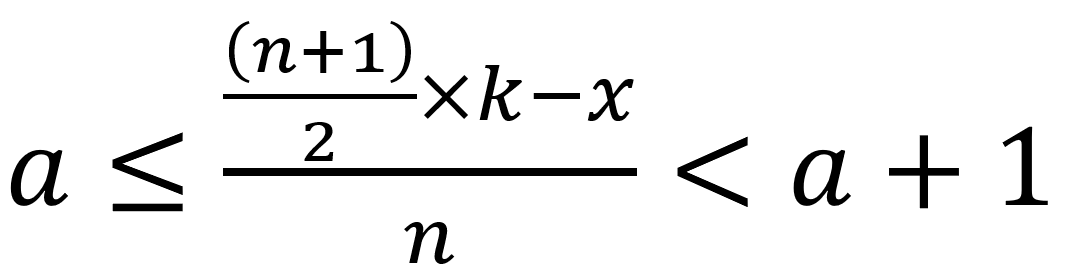，第𝑥張牌會移動至第a+1張牌，且洗牌一定次數後，目標牌會移動至第b+1張，奇數堆各偶數(2b)張撲克牌時，目標牌經由不斷洗牌後會移動至第b張或第b+1張並開始以此兩張牌重複循環。
2. 偶數(n)堆各(n+1)b 張撲克牌時，若目標牌為 x，當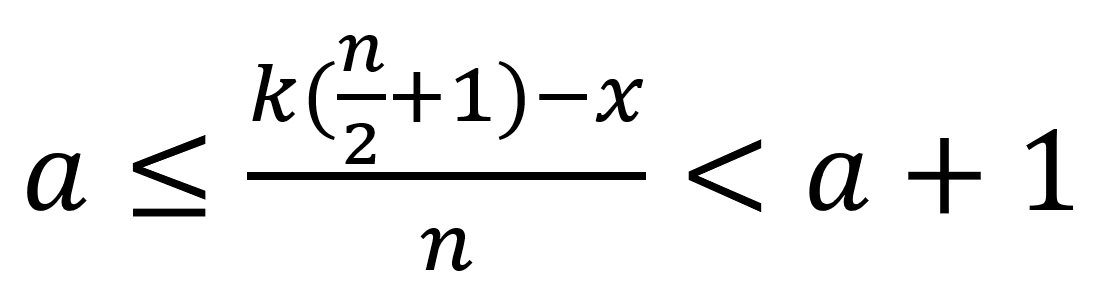，第 x 張牌會移動至第 a+1 張牌，且洗牌一定次數後，目標牌會移動至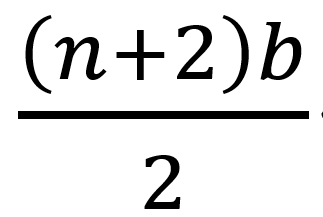第張或第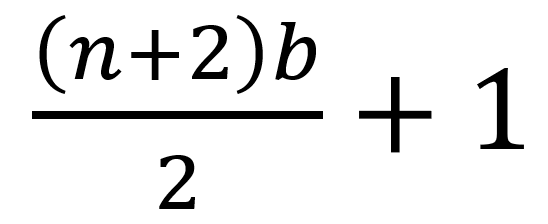張並開始以這兩張牌循環，偶數堆各(n+1)b+m 張牌時，m不論為偶數(2d)或奇數(2d+1)張，目標牌經由不斷洗牌後，會移動至第張牌。
3. 未來想研究目標牌在不同情況下，若想移動至目標位置，最少步數與n、k之間的關係。